3.7 隱微分
隱函數(implicit functions)
到目前為止,我們討論函數時,在其形式上,大部分指的是顯函數(explicit functions),意即可以用形式表達出來的,例如:或等,函數有另一種形式無法直接用形式表達,而只能透過與關係的描述(通常是一個與的方程式)來定義之,這樣的函數稱為隱函數(implicit functions),例如:,這個方程式可能隱藏著一個的實函數,使得,吾人稱此隱藏於其中的函數為隱函數。
例題1. 隱藏著幾個之函數?
【解】欲知隱藏著幾個之函數,最好的方法就是將這些函數明顯地找出來,亦即將隱函數化為顯函數,大部分的人會這樣做:
考慮定義域為最大的範圍,有個函數隱藏於其中,分別為、,其圖形如圖一(b)與(c)所示。但是,正確答案是無窮多個,讓我造出第三個給你看:
其圖形如圖一(d)所示,也滿足,也是隱藏於其中的一個函數啊!只不過他是一個不連續函數罷了,不連續點為處,若不連續點改為其他點,則我們有無窮多種選擇,可造出無窮多個類似之函數。當然,若題目改為隱藏著幾個之連續函數,則答案只有與兩個。 █
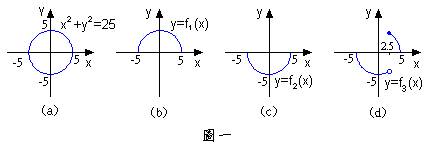
通常一個與之方程式,隱藏著不只一個之函數,像例題1就是,但有時候只隱藏一個之函數,像就是。可分解為
,
在考慮實函數之情況下,只隱藏一個之函數。此外,一個與之方程式也可能沒有任何實函數隱藏於其中,例如:,它是不可能找出任何來滿足該方程式的。
隱函數微分
像例題1中,隱藏著之函數,如今我們欲求其對之微分,之前的方法要先根據例題1先找出隱藏於其中的兩個連續函數與 ,再利用微分公式與連鎖律求其微分,答案是 與。但是若給你這樣的方程式:,其中隱藏著之函數,請你求出其對之微分,這就麻煩了,因為要將其中之隱函數明白寫成之顯函數形式已經非常困難了,遑論求其微分,所以我們需要一套隱函數微分法來求解此類的微分,這方法就是利用連鎖律直接將方程式對微分,再解出即是,詳細過程請看下列例題說明:
例題2.若,(a)求,(b)求此圓上一點之切線方程式。
【解】(a)
(利用連鎖律,記得是之函數)
解出
這個答案與之前與的答案相符,因為將代入即是。
(b)
故其切線方程式為或。 █
從以上例題這個答案可以看出隱函數微分的結果通常會保留有,這是與顯函數微分的結果只是的函數(例如:與)形式上不相同之處。不過想想卻是十分合理,一旦你可以找出之顯函數代入,則微分結果立刻變為完全只有之數學式了。
例題3.若,求。
【解】利用隱函數微分法,
(記得是之函數,再利用連鎖律)
解出。 ■
或許你會很好奇以上例題有無辦法用顯函數之形式表達?要這樣做先得找出其中的顯函數。這得先將看成是一個的一元三次方程式(把看做常數),再利用一元三次方程式根的公式求出,不過一元三次方程式根的公式十分難記(不像一元二次方程式根的公式那麼好記),我們查公式代入得到其三個根、、:
、
然後再將上述、、分別對求微分即是。天啊!這是多累的一件事啊!所以有時候雖可求得顯微分,但相比起來隱微分的計算容易多了。之圖形請參考圖二(a),我們於其中可找出隱藏的三個函數如圖二(b)、(c)、(d)所示。
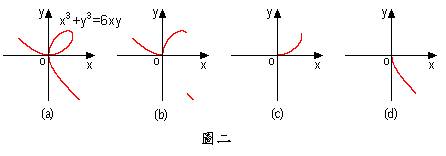
例題4.若,求。
【解】
解出 ■
兩曲線之正交
若兩曲線相交之處,各自的切線互相垂直,則稱此兩曲線正交(orthogonal)
例題5.試證,,與,,兩曲線群正交。
【證】若,則
解出。
同理,若,則
解出。
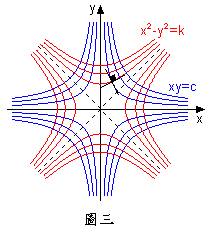
若與相交於,則此處各自切線斜率為與,兩者之乘積為,亦即此二切線互相垂直,故此二曲線群正交(參考圖三)。
3.7 習題(*表較難者)
1.已知,試求。
2.求上一點之切線方程式。
3*.試證微分公式中之冪次定律,為有理數。
4. 試證與此二曲線群正交。