3.3 微分公式
在3.1 微分當中，我們介紹了微分的定義，3.2 微分函數當中介紹了微分函數的觀念。我們欲求一函數之微分函數（或稱導函數），每每須由下列定義來求：
（1）
過程中需要用到各種極限定律，計算往往冗長不便，在本節中，我們將介紹一些微分公式以替代上述直接由定義求微分的方式，可節省我們很多時間與力氣。
3.3.1 微分公式
（1）為一常數，
（2）
（3）冪次定律：若為一整數，則
（4）若為一常數，可微分，則
（5）加法定律：若與皆可微分，則
（6）減法定律：若與皆可微分，則
（7）乘法定律：若與皆可微分，則
（8）除法定律：若與皆可微分，則
【證明】這些微分公式皆可由式（1）證明：
（1）令，，
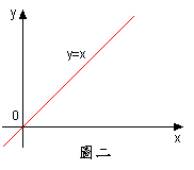其直觀意義可由圖一中函數圖形每一點之切線皆為水平得到驗證。
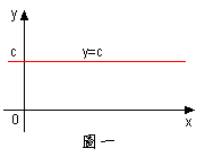
（2）令，，
其直觀意義可由圖二中函數圖形得到驗證。
（3）令，
在此 限制為正整數，稍後我們可將此推廣至整數，在3.7隱微分中又可將此推廣至有理數，最後在7.4一般對數及指數函數可將此推廣最極至，亦即 為所有實數皆成立。
（4）令，
（5）令，
（6）同上，將“”改成“”即可同理推導之，讀者可自行練習。
（7） 令，
（8）令，
■
利用上述之除法定律，可將上述之冪次定律延伸至為整數之情形：
定理 3.3.2
若為一整數，則。
【證明】
（1）為正整數，證明如3.3.1。
（2） 時， ， ，左＝右，故得證。或許有人會注意到上述 有問題，當 時變成 不一定會等於 。沒錯，不過這時候有一個更大的問題要先研究，當 時，左邊的 我們都知道 的任何次方是 ，任何數的 次方是 ，那麼 是 還是 ？還是公平起見，取 為答案？這不是個小問題！我們要等到7.7不定型極限與羅必達定律才能回答，所以在此假設 ，避開此問題。
（3）為負整數時，令，則為一正整數，由3.3.1中羃次、除法定律及其他公式：
綜合上述（1）、（2）、（3），吾人可將羃次定律推廣至為整數。 ■
如前所述，事實上羃次定律可推廣至為實數之情形：
3.3.3 一般羃次定律
若為一實數，則。
雖然直覺上，推廣至實數好像是順理成章之事，但是此定律的證明卻要等到7.4一般對數與指數函數，因為你要先回答 是什麼？我們在中學都學過的整數次方是什麼，例如；的負整數次方又是什麼，例如；的有理數次方又是什麼，例如，而且我們學過如何用筆算出的小數，但是你如何定義的無理數次方，如呢？是否為個相乘呢？那麼個相乘又是什麼意思？這些問題都要先回答，然後才能談到上述定律的證明。目前我們不妨先接受這個定律，並用他來計算微分。
例題1.求
【解】
（由3.3.1之（4）、（5）、（6））
（由3.3.1（1）、（2）、（3））
■
例題2.若，求。
【解】由3.3.1（7）乘法定律，
另外，，由3.3.1（3）（4），
可驗證上述答案。 ■
例題3. ，求。
【解】由3.3.1（8）除法定律及其他：
■
例題4.求下列微分：
【解】由3.3.3
■
3.3習題
1. 求在處之切線方程式。
2. 雙曲線在何處有切線平行？
3. 若、、為可微分之函數，試證明。
4. 試求。
5. ，試問在何處可微分？試畫出與之圖形。