3.2 微分函數
在3.1節中，我們定義一函數在一定點之微分為
（1）
現在我們考慮為變動的情形，亦即將（1）中的常數用變數取代，可得到
（2）
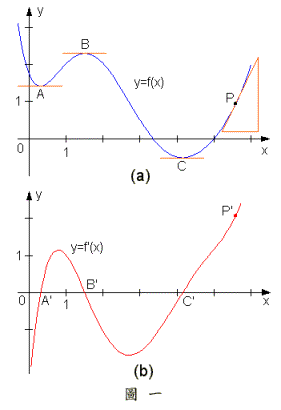
對上述極限存在的所有點，我們可形成一個的對應。由於極限存在時只有一個值，故上述的對應可視為一種函數的對應，吾人稱此一新的函數為 的微分函數。由3.1節， 之幾何意義為之曲線圖形在點之切線斜率，若已知一函數之圖形，我們可想辦法求出每一個點之切線斜率而畫出之圖形如圖一所示。值得注意的是之處即是切線為水平之處，之處即切線斜向上之處，而之處即切線斜向下之處。由於係根據（2）求得，故之定義域一般而言會小於之定義域，比較精確的說法是
的定義域的定義域 （3）
例題1.
（a）若，求，
（b）試畫出與之圖形對照比較之。
【解】
（a）
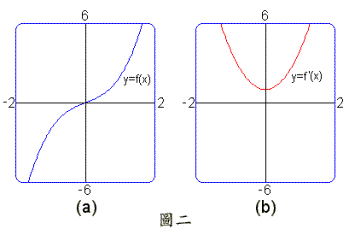
（b）與 之圖形如圖二（a）與（b）所示，我們也可以試試Java applet 030201 來觀察 與幾何上的關聯。 █
例題2.若，求之微分並找出之定義域。
【解】
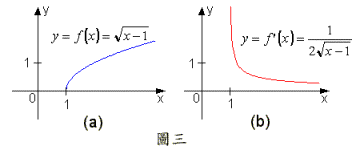當時，存在，故之定義域為，而之定義域為，的確滿足（3），在此與之圖形請參考圖三（a）與（b）。 ■
微分之記號
除此一記號外，之微分函數尚可記為：
或
其中、、皆稱為微分運算元（differential operator）代表微分之運算，而 此一記號由微積分的創始人萊布尼茲（Leibniz）所發明，若把它視為一個分數則其分子與分母各有涵義，詳細要等到3.10線性逼近與微分量中才會介紹，不過吾人可先由3.1節中微分的物理意義－瞬間變化率來領略一二：
此外，之記號亦可記為
3.2.1 可微分之定義
若存在，則稱在可微分（differentiable），此外在一開區間可微分，意即在此區間中每一點皆可微分，又在一閉區間可微分，意即在可微分，且在左端點為右邊可微（存在），在右端點為左邊可微（存在）。
例題3. 在何處可微分？
【解】
（i）當，，吾人選擇一個夠小的使得，則此時
故
在
可微分。
（ii）當
，
，吾人選擇一個夠小的
使得
，則此時
故
在
可微分。
（iii）當
，
討論其單邊極限，
，
，故
不存在，
不存在，
在
不可微分。
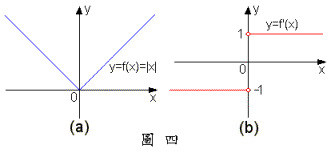綜合（i）-（iii），
可微分區域為
。此外，吾人可輕易地由圖四
與
印證此一結果。在圖四
中，
只在
處才有左切線與右切線不一致的情形，其餘則無此情形，意即
只在
處不可微分，其餘均可微分。 ■
定理3.2.2
在
點可微分
在
連續。
【證】欲證明
在
點連續，須證明
，或
，當
時，下式恆成立：
利用極限定律
故
，
在
連續。 ■
定理3.2.2告訴我們可微分推得連續，但我們要注意的是反推不成立，亦即若只告訴你
在
連續，則
在
可微分與否無法判斷。例如，例題3中
在所有實數皆連續，但卻在
處不可微分。吾人可將定理3.2.2擴展包含極限存在之情形如下：
定理 3.2.3
在
可微分
在
連續
存在。
也是一樣，要注意的是反推不成立。定理3.2.3的等價敘述常用於判斷不可微分之情形：
引理 3.2.4
不存在
在
不連續
在
不可微分。
常見不可微分的情形：
（i）不連續處：由引理3.2.4可得知，如圖五
所示，
（ii）轉折點（corner）：該點之兩個單邊微分皆存在，但左微分不等於右微分，亦即該點之左右切線不一致，如圖五
所示。例題3中，
處便是一個轉折點。
（iii）切線為垂直處：切線為垂直時，其斜率為
或
，亦即其微分值為
或
，故不存在亦即不可微分，如圖五
所示。
（iv）尖點（cusp）：為（ii）與（iii）之混合體，如圖五
所示。在圖五
中，
而
，亦即在
處左切線斜率為
，右切線斜率為
，左、右切線表面上看起來一致，但“內涵”卻不一致。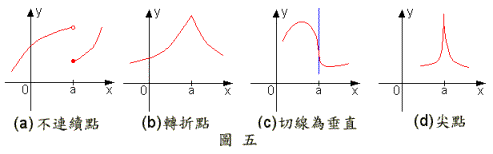
3.2習題（＊為較難者）
1. 若
，求
。
2＊.試問
在何處不可微分，其不可微分之類別為何？
3＊.
之圖形如圖六所示，試判斷下列敘述之對錯：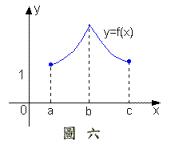
（i）
在
可微分，
（ii）
在
可微分，
（iii）
在
可微分。
4.試畫出
之圖形，並由切線斜率之觀念，大略畫出
之圖形。