2.5 連續性
預備知識
從圖形上來判斷函數的連續性很簡單：若之曲線圖形在這個點沒有斷掉，則稱在連續，否則在不連續。由此，引申出連續性正式的數學定義如下：
2.5.1 連續的定義
在連續。
以圖一為例，之圖形在處沒有斷掉，故在連續。而的確在處，成立。又由定義2.5.1推得，在不連續的充要條件即是不成立，這有以下幾種可能：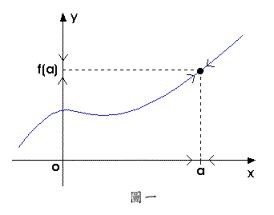
1. 沒有定義，
2. 不存在，
3. 有定義，亦存在，但。我們可以從下列的例子中探討不連續的情形。
2.5.2 單邊連續的定義
在左連續，
在右連續。
例題1：下列函數在哪些地方不連續？
【解】
（a） 沒有定義，故在不連續。
（b） 雖然有定義，但不存在，故在不連續。
（c） 雖然有定義，且存在但，故在 還是不連續。此題可試試Java applet 020501。
（d） 在所有整數點不連續，此因，， ，不存在，故 在所有整數點不連續。此題可試試Java applet 020502。以上各小題之結果可由圖二印証之。 ■
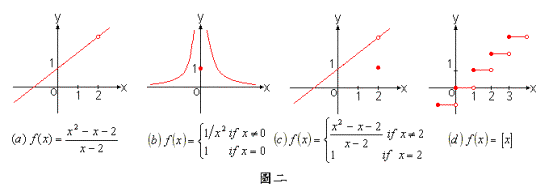
例題1中（a）與（c）這類的不連續，吾人稱之為可移除之不連續（removable discontinuity），因為只要我們定義或重新定義即可使得在處為連續。（b）這類的不連續稱為 無窮大的不連續（infinite discontinuity），而（d）這類的不連續稱為 跳躍式的不連續（jump discontinuity）。基本上不連續大致可分為這三類。
左右連續的概念係因應極限只考慮左極限或右極限時而產生的。例如，例題1（d）中，在任意整數點雖不連續，但卻是右連續，因為。
2.5.3 區間連續的定義
若在一區間的內部每一點皆連續，而在端點滿足單邊連續（左端點滿足右連續，右端點滿足左連續），則在此區間連續。在右連續。
例題2：試証在連續。
【解】對任意，由極限定律，
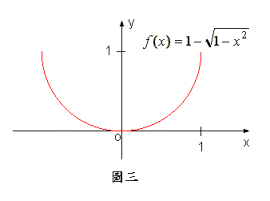
故在連續；又
，在左端點處為右連續；，在右端點1處為左連續。故根據定義2.5.3，在連續。此結果亦可由圖三印証之。 ■
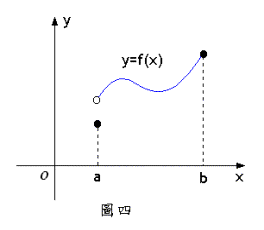例題3：之圖形如圖四所示，試分別討論在此四區間是否連續？
【解】在連續，因為，。
在不連續，因為在左端點不為右連續，亦即。
在連續，因為在連續，且在右端點為左連續，亦即。
在不連續，因為在左端點不為右連續。 ■
2.5.4 定理
若與在連續，為一常數，則下列函數亦在連續：
1. 2. 3. 4. 5. ，若。
【證明】我們可以利用極限定律證明之，在此只證明第一部分 之情形，其餘可類推。已知與在連續，故， 。
因此
（極限定律 2.3.1）
（上述已知）
故在連續。 ■
【證明】
（a）任何多項式皆可表為下式：
其中為常數，利用極限定律，對任一實數，我們可推得：
（極限定律1）
（極限定律3）
（極限定律7、8、9）
故在任一實數連續，亦即在連續。
（b）若唯一有理函數，則可表為。
其中，與為多項式函數，又之定義域為，利用極限定律及（a）之結果對任一實數，我們可推得：
（極限定律5，在此）
（( ）之結果）
故在任一實數連續，亦即在其定義域連續。 ■
例題4：求
【解】利用2.5.5定理，我們不再需要像2.3節中利用極限定律一步步繁瑣的求解。為一有理函數，其定義域。根據定理2.5.5（b），在其定義域連續，而，故在連續，因此。 ■
2.5.6 定理
下列型態之函數皆在其定義域連續：
多項式函數、有理函數、根號函數、三角函數。
此定理可視為2.5.5之推廣，在此省略其證明。
例題5：在何處連續？
【解】在連續，在連續，在連續，故在此三者之交集，亦即連續。 ■
2.5.7 定理
若在連續，且，則，換言之亦即
。
直觀上，此定理不難理解，因為當靠近時，會靠近，而在連續，故當靠近時，則會靠近 。但其詳細證明須使用2.4節極限的精確定義來證明，過程較為繁瑣在此省略。
2.5.8 定理
若在連續，在連續，則兩者之合成函數在連續。
【證明】已知在連續，故。又因在連續，利用2.5.7定理可得，亦即在連續。■
例題6：在何處連續？
2.5.9 中間值定理
若在一閉區間連續，且為任一介於與之間的實數，則存在一個，使得。
【解】可視為，或，其中，，，，而上述諸函數接在其定義域上連續，故在其定義域連續，亦即在連續。■
中間值定理之證明超出本書之範圍，在此省略，不過我們可以用圖形來體會此一定理。如圖五所示，在連續，介於與之間，則根據中間值定理，我們可以在中，至少找到一個，使得。圖五中，這樣的只有一個，而圖五中，這樣的有三個。
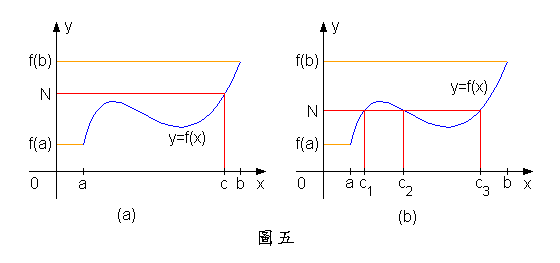
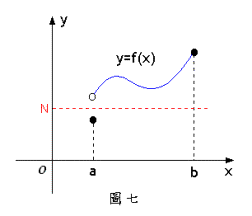
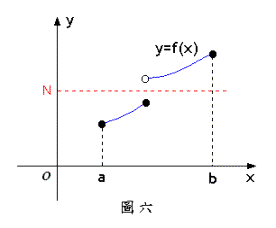
此外，我們也可以利用 Java applet 020503 來做實驗，加強對中間值定理的了解。 中間值定理的結果若要成立，“閉區間”與“連續”這兩個條件缺一不可。若 如圖六般之不連續，選擇如圖中之值，則無法在中找到一個，使得。又如圖七，只在連續，但在不連續，當我們選擇如圖七中之值時，便無法在中找到一個，使得。
例題8：試證方程式在與之間有一根。
【證明】令，因為一多項式函數，故在連續，因此也會在連續。在此選擇，此值介於與之間。根據中間值定理，存在一個，使得，亦即我們至少可在中找到一個方程式的根。 ■
2.5習題(＊表較難之題目)
1. ，試證明在連續。
2. ，若在連續，則值為何？
3 . ，試問在何處連續？
4 . ，試問在何處連續？
5 . 一西藏喇嘛早上七點從其山腳下的修練所出發，走唯一的山路上山，於晚上七點到達山頂。翌日，早上七點從山頂下山，晚上七點時抵達山腳下的修練所，試用中間值定理證明，在此山路的某一處，這個喇嘛上山及下山經過該處都是在一天的同一時刻。