2.3 以極限定律求極限
在2.2節，我們利用觀察法與畫圖法求極限值實在很不方便，以下我們將介紹一些極限定律，利用這些極限定律來計算極限值就輕鬆多了。
2.3.1極限定律
若為一常數，與皆存在，則
1.
2.
3.
4.
5. ，其中
6. ，為正整數
7.
8.
9. ，為正整數
10. ，為正整數（若為偶數，則必須額外假設）
11. ，為正整數（若為偶數，則必須額外假設）
以上每一條極限定律在直觀上都很容易接受，至於他們的證明，則需要到2.4節 極限精確定義 才會提到。這裡我們先理所當然地接受，利用他們來計算極限。
例題1：試利用極限定律求下列極限：
【解】
（定律2、1）
（定律3）
（定律9、8、7）
最後答案看似將代入 即是，但誠如我們在2.2節中再三強調極限與函數值二者定義上是完全不同的。當然你計算答案時可以直接代入去求，但你要宣稱是根據極限定律推得的。
（定律5）
（定律1、2、3）
（定律9、8、7）
■
同(a)，結果跟直接代入一樣，由這樣的結果我們可以引出下列的定理：
定理 2.3.2
若為一多項式或有理函數，在之定義域中，則。
上述的定理告訴我們，當函數為多項式或有理函數時，極限值會等於函數值。這裡所謂的有理函數又稱為分數函數，即分子與分母皆為多項式之函數，像例題1的（b）即是。多項式函數的定義域為，而有理函數的定義域為所有使分母不為之實數所成的集合。上述定理可輕易地用極限定律證明之，我們把它放在習題中（習題1.2）。
例題2：試求
【解】若令，則為一有理數函數，在此我們不能用定理2.3.2，因為0不屬於之定義域中。先將其化簡：
（注意：最後一步之所以成立係，但永遠，故可以約分。這細節雖小，觀念上卻很重要。）最後，
（定理 2.3.2） ■
例題3：試求
【解】我們不能直接使用極限定律5，因為分母的極限為0，故要先想辦法化簡。我們試將分子有理化：
（注意：等號成立之條件為 0，這樣與才能約分。）接下來，
上式
（注意：最後一步與約分要成立需要求，而在此，但永遠都不會為0，故條件成立。）
接下來利用極限定律：
上式 （定律5、1）
（定律11）
（定律7、定理2.3.2）
■
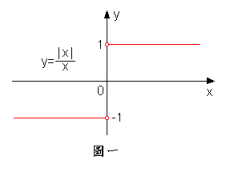
例題4：試証不存在。
【證】
右極限≠左極限，根據2.2節定理2.2.4， 不存在。
之圖形請參考圖一。■
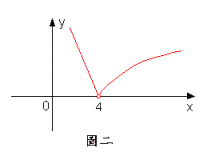
例題5：若，試決定是否存在？
【解】
右極限＝左極限＝0，故。 之圖形請參可圖二。■
接下來介紹兩個關於極限的定理:
定理 2.3.3
若，當靠近時（本身可例外），且與皆存在，則。
這個定理的推論很明顯，證明在此省略，若要證明需要用到2.4節極限精確定義來證。
|
定理2.2.4 夾擠定理 若，當靠近時（本身可例外），且，則。 |
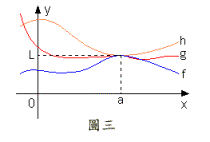參考圖三，夾在與之間，當時，則無可避免地會被夾擠而使得
亦得成立，故名之為夾擠定理。這個定理的證明亦需要用到2.4節極限精確定義，在此省略。夾擠定理在數學證明上是一個很好用的工具，今以下列例題闡述之：
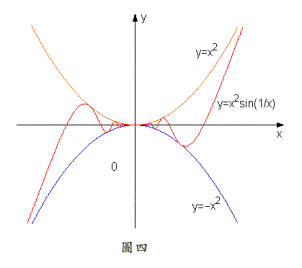
例題10：試證
【證】我們不能直接用極限定律，因為不存在(為什麼？自己想想看)。先觀察下列的事實:
其中，由夾擠定理，
。被與夾擠的情形，請參考圖四。
2.3 習題
1. 求。
2. 求。
3. 若 求
。
4. 試證。