一•三角函數的起源
三角學的概念起源甚早,在古文獻「萊因德紙草書」出土後證據顯示古埃及人己有實用三角學的粗略概念,來保持金字塔每邊都有相同的斜度,只是當時並沒有使用餘切這個名詞而已。至西元前150年至100年間,希臘人熱衷天文學,開始研究三角學,於是三角學漸漸有了雛形。
後來印度人吸收了希臘人在三角學方面的知識,再加以改進,也把它當成研究天文學的利器。長久以來,三角學就這樣依附著天文學發展,直到十三世紀,才自天文學中脫離成一門獨立的學問。十六世紀的歐洲,由於航海、曆法計算的需要,更增加三角學的重要性。如今它不但應用於天文、地理,舉凡航海、航空、建築、工程、體育等…的一門基礎學問,甚至在我們日常生活中,也成為不可欠缺的知識。
二•角
希臘數學家歐幾里得在所著「幾何原本」這一書中說明一個平面角,就是平面上兩條相交但不重疊的直線,彼此間傾斜度。實際上角的概念,一方面代表兩條相交直線分割的性質,另一方面也代表其分割程度,即角的度量衡。
三•角的度量與換算
1.![]() 制
制
我們都知道圓規繞一圈為360度,但是好奇而且追根就底的人就會有疑問,為什麼會將圓分割為360等分。從數學史的角度,也許給一些答案,古代巴比倫人計數的單位為60進位,而且在60倍數中最接近一年的天數為360。可能符合上述的解答,即使在日常生活以10進位的時代,時鐘的刻度還保持60進位,規定1小時為60分鐘,1分鐘為60秒。
2.弳度制(弧度)
在上一節,我們找圓分割為360等分,每一等分記為1度,1圈總計為![]() 。
。
 |
數學上還有一種常用的度量單位,稱為弧度。在圓周上,截取與半徑等長之弧,則此弧所對的圓心角稱為一弧度(或稱為一弳),以弧度為單位,通常省略不寫,如:2弧度簡記為2(圖1)
又因為單位圓的周長為![]() ,所以
,所以![]() =
=![]() ,由此可得1弳度
,由此可得1弳度![]() ,且
,且![]() (弧度),這裡有一個有趣的結果,經掌上型計算器可得知
(弧度),這裡有一個有趣的結果,經掌上型計算器可得知![]() ,這與
,這與![]() 的差距不到十萬分之一。所以當弳度x為很小時,
的差距不到十萬分之一。所以當弳度x為很小時,![]() 換句話說計算sinx可用x來估計,這可能是弳度被多人接受的原因之一且
換句話說計算sinx可用x來估計,這可能是弳度被多人接受的原因之一且![]() 在微積分上有重要的應用。
在微積分上有重要的應用。
四• 有向角
沒有人知道為什麼量角度要採逆時針方向,或許從觀察大自然的現象,可略知一二,例如,因受磁場的影響在北半球的水槽的水以逆時鐘方向流出,但在南半球的水槽則順時鐘方向流出,這種水流的方向是有差別。再舉一例:
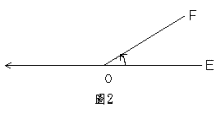 |
設
如果![]() 表東方,
表東方,![]() 表東北方,我們可用
表東北方,我們可用![]() 表示從東方到東北方的方位差。如果站在O點,面向東然後轉到東北方位與先面對東北方位然後轉到東方,這兩起動作是有區別的。為了能夠把這些差異之處也表現出來,我們只好對角的兩邊
表示從東方到東北方的方位差。如果站在O點,面向東然後轉到東北方位與先面對東北方位然後轉到東方,這兩起動作是有區別的。為了能夠把這些差異之處也表現出來,我們只好對角的兩邊![]() 與給
與給![]() 出先後次序,把一個稱為始邊,另一個稱為終邊。例如,從
出先後次序,把一個稱為始邊,另一個稱為終邊。例如,從![]() 轉至時
轉至時![]() ,
,
![]() 是始邊,
是始邊,![]() 就是終邊。從始邊轉向終邊就是旋轉方向,此時就可以把角看作是由始邊沿著旋轉方向到終邊的旋轉量。為了方便,通常規定逆時鐘方向為正,順時鐘方向負,則把旋轉方向是正的角稱為正向角,簡稱正角;旋轉方向是負的角稱為負向角,簡稱為負角。正向角與負向角合稱為有向角。例如,從東轉至東北方位的有向角是
就是終邊。從始邊轉向終邊就是旋轉方向,此時就可以把角看作是由始邊沿著旋轉方向到終邊的旋轉量。為了方便,通常規定逆時鐘方向為正,順時鐘方向負,則把旋轉方向是正的角稱為正向角,簡稱正角;旋轉方向是負的角稱為負向角,簡稱為負角。正向角與負向角合稱為有向角。例如,從東轉至東北方位的有向角是![]() ,從東轉至東南方位的有向角是
,從東轉至東南方位的有向角是![]() ,如下圖3所示:
,如下圖3所示:
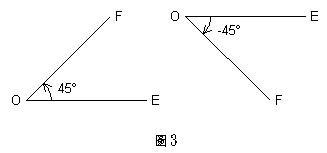
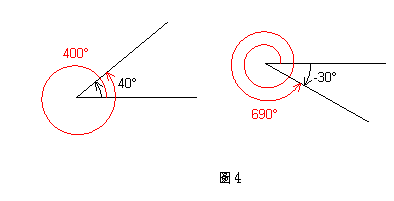
在有向角中,有相同始邊及終邊的角,互稱為同界角。兩個同界角之間一定相差![]() 的倍數,如下圖4中的
的倍數,如下圖4中的![]() 角與
角與![]() 角,
角,![]() 角與
角與![]() 角都是一對同界角。
角都是一對同界角。
五•銳角的三角函數
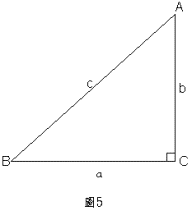 |
在國中的時候,我們曾利用相似三角形的性質引進了銳角三角函數來解決實際的測量問題。現在我們先把這些函數定義複習之後,再將其推廣到廣義角的三角函數。設
其中![]() 為直角,
為直角,![]() 為斜邊,兩股
為斜邊,兩股![]() 與
與![]() 分別是
分別是![]() 的鄰邊與對邊。
的鄰邊與對邊。
設![]() ,
,![]() ,
,![]() ,則我們定義
,則我們定義![]() 的六個三角函數如下:
的六個三角函數如下:
![]()
![]()
![]()
![]()
![]()
![]()
從上述的定義,若令![]() ,我們可得下列關係式:
,我們可得下列關係式:
一•倒數關係式
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
二•商數關係式
![]() ,
, ![]()
三•平方關係式
利用畢氏定理,可得
![]()
![]()
![]()
四•餘角關係式
如圖5所示,![]() 為一直角三角形,
為一直角三角形,![]() 為直角,因為三角形的內角和為
為直角,因為三角形的內角和為![]() ,所以
,所以![]() 和
和![]() 互為餘角,即
互為餘角,即![]() ,
,![]() 的對邊b恰為
的對邊b恰為![]() 的鄰邊,由正弦和餘弦的定義可知
的鄰邊,由正弦和餘弦的定義可知
![]()
同理可得
![]() ,
,![]()
![]() ,
,![]()
![]()
故可得下列關係:
![]()
![]()
![]()
![]()
![]()
![]()
六•廣義角的三角函數
我們在前面中引進了有向角的概念後,在本節中準備定義廣義角的三角函數。設![]() 為有向角,把它的頂點放在原點,始邊放在x軸的正向上,然後看它的終邊落在何處,終邊可能落在第一象限,也可能落在第二象限、第三象限或第四象限,如圖6所示,圖上的均為正向角且小於
為有向角,把它的頂點放在原點,始邊放在x軸的正向上,然後看它的終邊落在何處,終邊可能落在第一象限,也可能落在第二象限、第三象限或第四象限,如圖6所示,圖上的均為正向角且小於![]()
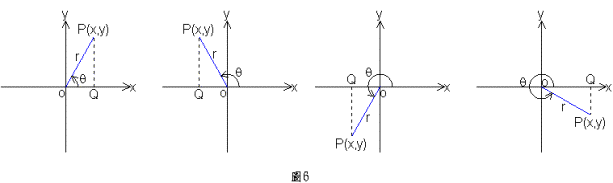
當然,終邊也可能落在x軸或y軸上。無論如何,在終邊上任取異於0的一點P,設其坐標為(x,y),並令![]() ,雖然x和y可正、可負或為零,但是r恆為正。現在用x,y和r這三個數來定義廣義角的三角函數如下:
,雖然x和y可正、可負或為零,但是r恆為正。現在用x,y和r這三個數來定義廣義角的三角函數如下:
![]()
![]()
![]()
![]()
![]()
![]()
值得注意的是,我們要在它的比值有意義的情況下才能定義廣義三角函數,否則視為沒有意義。例如,當P點在x軸上時,則P點的y坐標為0,此時,![]() 和
和
![]() 的分母都是0,這種比值是沒有意義的。又當P點在y軸上時,則P點的x坐標為0,此時,
的分母都是0,這種比值是沒有意義的。又當P點在y軸上時,則P點的x坐標為0,此時,![]() 和
和![]() 的分母都是0,也是沒有意義的。事實上,只有P點在x軸或y軸上的時候才會有比值沒有意義的情形發生。
的分母都是0,也是沒有意義的。事實上,只有P點在x軸或y軸上的時候才會有比值沒有意義的情形發生。
當![]() 為銳角時,相應於直角三角形
為銳角時,相應於直角三角形![]() 的各量x和y都是正的,所以上面的定義和銳角三角函數定義完全相同。
的各量x和y都是正的,所以上面的定義和銳角三角函數定義完全相同。
根據上述廣義角三角函數的定義,我們可繪製六個三角函數的圖形,他們都是週期函數,圖形如下列的Java applet所示:
例:試求![]() ,
,
![]() ,
,![]()
解:
 |
設
在終邊上任取一點P,令![]() ,並作
,並作![]() ,顯而易見
,顯而易見![]() ,所以P的坐標為
,所以P的坐標為
![]() ,
, ![]()
故
![]()
![]()
![]()
試求(1) ![]() ,
,![]() ,
,![]()
(2) ![]() ,
,![]() ,
,![]()
從廣義角的三角函數的定義可知,凡是同界角均有相同的三角函數值。所以下列公式成立:若n為一整數,則
![]()
![]()
![]()
![]()
![]()
![]()
我們利用這些性質可以把任意角的三角函數化成![]() 到
到![]() 之間的三角函數。例如,
之間的三角函數。例如,
![]()
![]()
例題:
化下列諸角的三角函數為![]() 到
到![]() 之間的三角函數:
之間的三角函數:
![]() ,
, ![]() ,
,![]()
我們把以原點為圓心而半徑為1的圓稱為單位圓。設![]() 與
與![]() 兩個角的終邊與單位圓的交點分別為
兩個角的終邊與單位圓的交點分別為![]() 與
與![]() ,如圖8所示:
,如圖8所示:
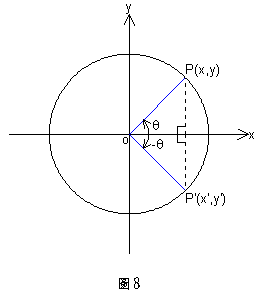
因為![]() 與
與![]() 對稱於x軸,所以
對稱於x軸,所以
![]() ,
,![]()
故
![]()
![]()
![]()
![]()
![]()
![]()
我們利用這些性質可以把負角的三角函數化為正角的三角函數。例如,
![]()
![]()
設![]() 與
與![]() 兩個角的終邊與單位圓的交點分別為
兩個角的終邊與單位圓的交點分別為![]() 與
與![]() ,如圖9所示:
,如圖9所示:
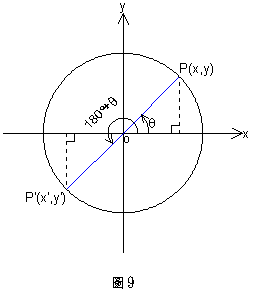
因為![]() 與
與![]() 對於原點0成對稱,所以
對於原點0成對稱,所以
![]() ,
,![]()
故有
![]()
![]()
![]()
![]()
![]()
![]()
例如
![]()
![]()
設![]() 與
與![]() 兩個角的終邊與單位圓的交點分別為
兩個角的終邊與單位圓的交點分別為![]() 與
與![]() ,如圖10
,如圖10
所示:
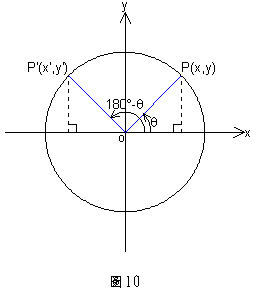
因為![]() 與
與![]() 對於y軸成對稱,所以
對於y軸成對稱,所以
![]() ,
,![]()
故有
![]()
![]()
![]()
![]()
![]()
![]()
例如
![]()
![]()
例題:
證明下列關係式:
![]() ,
, ![]()
![]() ,
, ![]()
你可以利用下面的 Java applet 算你想要的六個三角函數值 :