3.1 微分（Derivatives）
3.1.1 微分的定義
函數在之微分記為，定義如下：
（1）
若（1）中極限存在，則稱在可微分（differentiable），否則稱在不可微分。很明顯地，計算此極限時，直接代入會得到，故需要借助極限定律方能得解。上述定義的另外一個等價的表示法為
(2)
例題1：求在之微分。
【解】我們可根據（1）或（2）來求，先根據（1），
或根據（2），
■
微分的幾何定義
曲線在處之切線斜率等於。
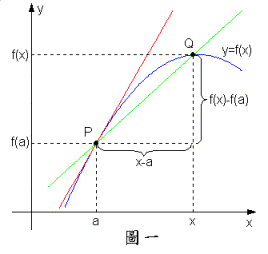由圖一所示，點之座標為，點之座標為。之斜率為，當時，，在點之切線，亦即在點切線的斜率，又由(2)
， ，故曲線在處之切線斜率等於，而此切線方程式為。
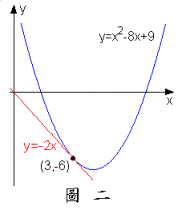
例題2：求拋物線在處之切線方程式。
【解】令，根據例題1，，故在處之切線斜率為，其切線方程式為
或 (圖形如圖二所示) 。
■
微分的物理意義
微分可視為對在處之瞬間變化率。
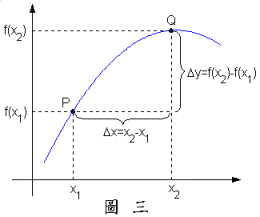由圖三，當由變動至，的變化量記為（記得是變化後減掉變化前）。相對的，由變化至，的變化量記為。變化量對變化量的比率簡稱為對
的變化率，記為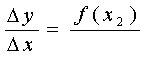
。其與微分的關係為
。其中，
稱為
對
在
的“瞬間”變化率，由上述關係即是
。為能更進一步地了解此義，我們不妨套用牛頓的運動定律，若
表示位置，
表示時間，
即為位置對時間的函數。如此，
表示時間的變化量，
表示在時間
的位置變化量，即所謂的位移。位置對時間的變化率，
，牛頓稱為速度，在時間
的平均速度；而其瞬時變化率
，牛頓稱為在
的瞬時速度，簡稱速度。速度是向量的觀念，方向由其值的正負來表示；而速率指的是速度的大小，在
的速率為
。
例題3：一質點運動，其位置對時間的函數為
，
的單位為秒，
的單位為米，求
秒之速度與速率。
【解】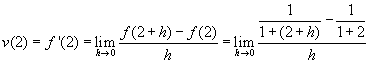
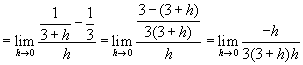
故在
秒之速度為
，速率為
。
■
3.1習題
1.
，求
並用以求曲線在
處之切線方程式。
2.
，求
。
3.將下列極限表為
，試問
與
各為什麼？
（1）
（2）
4.在一細菌生長實驗室中，細菌個數
對時間
的函數為
，
（a）
之意義為何？他的單位是什麼？
（b）若細菌生長過程中，空間與養份的供給不受限制，試問
與
孰大？若養分供給有限，則結論是否有變？試論述之。