2.2 函數的極限
2.2.1 極限的直觀定義
唸做“當x趨近於a時,f (x)之極限為L”,意即“只要x夠靠近a,但,f (x)可任意地接近L”。
上述 亦可表為 ,當,
唸做“當x趨近於a時,f (x)之值趨近於L”。
這裡要注意的是“”這句話,極限研究的是x靠近a時,f (x)的行為。基本上與f (a)無關,如果詳細討論與f (a)之間的關係,可分成表一中的五種關係:

表一
其中值得注意的是,即使f (a)與都存在時,還可進一步分成兩者相等或不等,在研究下面一連串例子時,希望讀者把這張表放在心上。
例題1:試求
【解】讓我們令,求上述極限時,你可能會有一股衝動想把2代到,亦即找出,而它即是。這種觀念是很危險的,記得表一中 只是五種可能的一種,再還沒有學到2.3節的極限定律時,正確的做法是利用觀察法或畫圖法。
(一)觀察法
用計算機算出一連串x靠近2時之值,記得你要多靠近2都可以,但就是不能算。將這些數據排列起來觀察,如表二你可以觀察出不論x比2大或比2小,x趨近於2時,“好像”會趨近於2,因此我們推論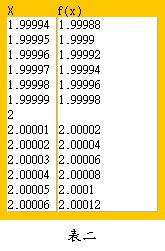 。表二是由Java
applet 020201算出來的,有興趣可以玩玩看。
。表二是由Java
applet 020201算出來的,有興趣可以玩玩看。
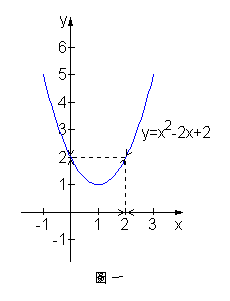 也許你觀察到上述極限值明明就是函數值,為何不一開始將2直接代入就好了,還要這麼麻煩? 記得極限的定義是“x很靠近2,但”,直接代入易養成觀念上的錯誤。
也許你觀察到上述極限值明明就是函數值,為何不一開始將2直接代入就好了,還要這麼麻煩? 記得極限的定義是“x很靠近2,但”,直接代入易養成觀念上的錯誤。
(二)畫圖法
之圖形是拋物線不難畫,其圖形如圖一所示。由圖一,當x不論從比2小或比2大趨近於2時,但,的確會趨近於2,故亦可推論出。你也許認為畫圖法比觀察法容易求得極限,觀察法好像比較囉唆。事實的確如此,但那是函數的圖形很容易畫的情況下,若函數圖形很難畫時,就只能靠觀察法了。
在此例題中,與f (2)二者皆存在,且,對照表一是屬於函數值與極限值俱存在且二者相等的情況。 █
例題2:試求
【解】 讓我們令,這時如果你還是習慣將1代入就行不通了。將1代入得到,你會說是“無意義”,也就是說f (1)這個函數值未定義。另外,希望你不會犯約分為1這種“致命”的錯誤。這裡有一個廿世紀初印度天才數學家Bhaskara的故事,Bhaskara從小就聰穎過人,在唸小學,數學老師交到分數中約分的觀念時,以分蘋果說明。數學老師說如果我有5個蘋果,分給5位同學,每個同學可得到一個蘋果,所以。推廣來說如果我有n個蘋果給n位同學,每個同學皆可得到一個蘋果,所以
。這時Bhaskara看出n要不為0才行,馬上提出異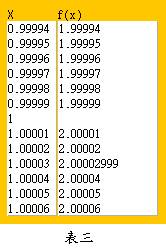 議說「老師,照你的推論,如果你沒有蘋果,也不分給任何一位同學,結果是每個同學還是可以得到一個蘋果囉?」當場讓數學老師啞口無言。 言歸正傳,我們依舊用觀察法與畫圖法找出極限。
議說「老師,照你的推論,如果你沒有蘋果,也不分給任何一位同學,結果是每個同學還是可以得到一個蘋果囉?」當場讓數學老師啞口無言。 言歸正傳,我們依舊用觀察法與畫圖法找出極限。
(一)觀察法
用計算機計算一連串x靠近1,但 之函數值f (x),如表三所示。由表三可觀察出極限值“好像”會是2。表三是由Java applet 020202算出來的,有興趣可以玩玩看。
(二)畫圖法
之圖形比較難畫,須稍微推理一下:。
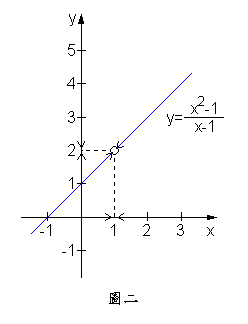 上式約分就得,細心的同學會提出萬一,不就犯了的錯誤嗎?沒錯,所以我們要分與兩種情形。
上式約分就得,細心的同學會提出萬一,不就犯了的錯誤嗎?沒錯,所以我們要分與兩種情形。
的圖形就比較好畫了,畫起來如圖二所示。 如圖二,當x不論從比1小或比1大趨近於1時,f (x)的確會趨近於2,故亦可推論出。本例題,對照表一,是屬於極限值存在但函數值不存在的情形。 █
例題3:試求
【解】
 (一)觀察法
(一)觀察法
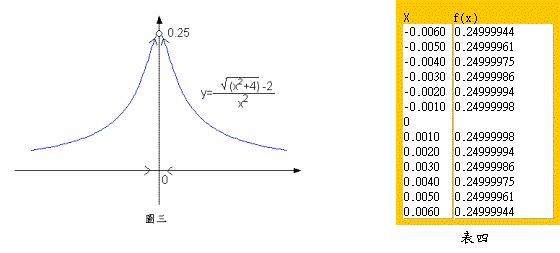
結果如表四(可試試其Java applet 020203),由此可推論出極限值應是 。
(二)畫圖法
之圖形也不好畫,要藉由電腦軟體來畫,如圖三所示。由圖三,的確當x趨近於0時,會趨近於。本例題是表一中,極限值存在但函數值不存在的情形。 █
例題4:試求
【解】(一)觀察法
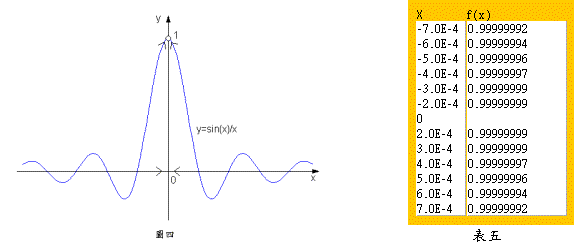 結果如表五(可試試其Java
applet 020204),由此可推論出極限值是1。
結果如表五(可試試其Java
applet 020204),由此可推論出極限值是1。
(二)畫圖法
之圖形也不好畫,在此利用電腦軟體畫出之圖形如圖四所示。由圖四,的確當x趨近於0時,會趨近於1。 本例題亦屬於表一中,極限值存在,函數值不存在的情形。 █
例題5:若 ,求。
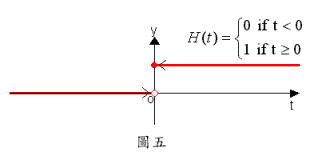 【解】這個函數的圖形很簡單,利用畫圖法即可。由圖五,當t比0小趨近於0時,會趨近於0,但當t比0大趨近於0時,會趨近於1。t=0左方極限值與右方極限值不一致,此時不存在(否則會有兩個極限值,那是定義所不允許的)。本例題不存在,但存在,這是表一中,函數值存在但極限值不存在之情形。 █
【解】這個函數的圖形很簡單,利用畫圖法即可。由圖五,當t比0小趨近於0時,會趨近於0,但當t比0大趨近於0時,會趨近於1。t=0左方極限值與右方極限值不一致,此時不存在(否則會有兩個極限值,那是定義所不允許的)。本例題不存在,但存在,這是表一中,函數值存在但極限值不存在之情形。 █
藉由例題五,我們來介紹一下所謂的單邊極限。
定義2.2.2 左極限的定義
唸做“當x從a之左邊趨近於a時,f (x)之極限為L”,意即只要x夠靠近a,但,f (x)可任意地接近L。
定義2.2.2其實只是定義2.2.1稍加修改而已,這裡係指x趨近於a,但x比a小。同理指的是x趨近於a,但x比a大。類似左極限定義的寫法,我們可寫出以下右極限的定義:
定義2.2.3 右極限的定義
唸做“當x從a之右邊趨近於a時,f (x)之極限為L”,意即只要x夠靠近a,但,f (x)可任意地接近L
左極限與右極限各管一邊的極限,故稱為單邊極限。例題5中的極限雖然不存在,但兩個單邊極限皆存在,分別為與,只是兩者不相等,故不存在,我們藉此引出下列的定理:
定理2.2.4
且 Û .
定理2.2.4告訴我們,所謂即是其兩個單邊極限都存在且皆等於L。 介紹完單邊極限,接下來我們來研究極限為無窮大之情形,無窮大的數學符號為¥,意指〝大的不得了〞,〝大的不受限制〞。¥是一個概念,而不是一個數字,這個觀念很重要,因為只要是一個數字,就會在實數線上有個位置,而¥無法在實數線上定位。同理-¥表示〝小的不得了〞,〝小得不受限制〞,他也只是一個概念,同樣無法在實數線上定位。
例題6:是否存在?
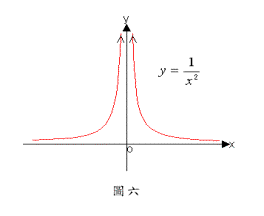 【解】由圖六,當x趨近於0時,f (x)會趨近¥,亦即,但這樣寫不要誤會他極限存在。因為如前所說的,¥不是一個數字,所以極限不存在,在此只是額外告訴我們不存在的原因是極限值為¥之故。這個例題是屬於表一中函數值與極限值皆不存在的情形。
█
【解】由圖六,當x趨近於0時,f (x)會趨近¥,亦即,但這樣寫不要誤會他極限存在。因為如前所說的,¥不是一個數字,所以極限不存在,在此只是額外告訴我們不存在的原因是極限值為¥之故。這個例題是屬於表一中函數值與極限值皆不存在的情形。
█
我們在此給極限為¥或-¥的情形一個正式的定義:
定義2.2.5 極限為¥的定義
若f在a附近皆有定義(a本身可除外),則,意即只要x夠靠近a,但,f (x)可任意地大。
定義2.2.6極限為-¥的定義
若f在a附近皆有定義(a本身可除外),則,意即只要x夠靠近a,但,f (x)可任意地小。
在圖六中,當x靠近0時(不管從a之左邊或右邊),函數之曲線會漸漸的靠近(即y軸),這時我們說為之垂直漸近線(vertical asymptote)。以下給垂直漸近線一個正式的定義(參考圖七):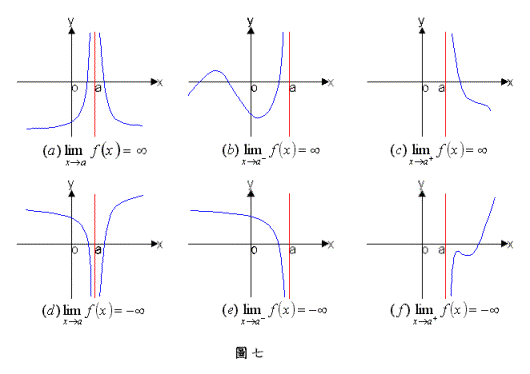
定義2.2.7 垂直漸近線(vertical asymptote)
若下列情況中,至少有一為真,則此直線為圖形之一垂直漸近線:
例題7:求之漸近線
【解】,以為例,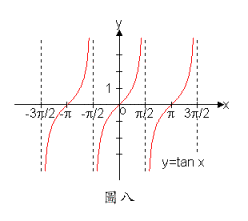
當時,,,故。
當時,,,∴。
意即,。同理在任何處亦是如此,故為之垂直漸近線(參考圖八)。 █
回顧表一中,還有一種情形的例子還沒有提到,就市函數值與極限值皆存在,但兩者不相等的情形,我們最後以下面的例題闡釋之。
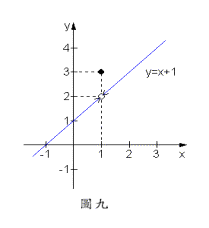 例題8:已知,求。
例題8:已知,求。
【解】此例題在1之極限值與例題2無異,因為在之極限值是不管函數值存在與否的。與例題2不同的地方是本例題屬於表一中極限存在,函數值亦存在,但兩者不相等的情形(參考圖九)。 █
2.2習題
1. 由圖十,試求在與5之左、右極限及完整的極限值,並分別指出他們是屬於表一中哪一種情形。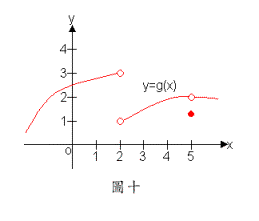
2. 定義為不超過x最大正整數,例如,,,試畫出的圖形,並據以判斷對任意一個整數n, 、、之值為何?它是屬於表一的那一種情形?